The Art of Optimising

Nutfreak/Freedom systems

1. Abstract As the reader progresses through the pages of this document, he will understand the necessity for optimizations in both his algorithm and his code. Various issues will be dealt with, such as algorithm implications: where are the common flaws that one should avoid, and how to speed up the thought process when designing a fast algorithm. The much debated issue of whether or not a compiler should be blindly followed regarding multi-pass optimizations, will be tackled both for short and lengthy algorithms. As well as the question when and where we should implement pure assembly code. Various examples of how you should implement C and ASM code will pass the revue, as well as how not to do this. Having read and understood these various parts, one can advance into the world of highly complex, but highly performant optimizations. One of them being the use of multi-pipeline optimization for superscalar processors like the Intel Pentium (and higher), AMD K5 (and higher) and the Motorola 68060 (and higher), to name a few mainstream CPU's. This will be dealt with at the assembly-language level only. In endings, a proposition is given to optimize code by using SIMD instructions on CPUs which do not have any SIMD (MMX, 3Dnow!, SSE, SSE2,...) instructions at the hardware level. 2. Preface Hello there dear Hugi readers. I have been a big fan of diskmags for the past 10 years already (starting at the C64 with the sex'n'crime diskmag - gosh I'm old hehe). After the great Imphobia ended (probably too afraid of the evil number 13 hehe), I kind of fell into a black hole. But luckily there was Hugi to spice up my scene life again. (ok ok, enough with the suck-ups already :)). Over the years, the scene has given me a lot of great times. I wasn't that big of a coder, but I had lots of fun. And that was the most important thing of all. So here I am to give something back... Especially to the newbies in the scene, although most veterans will also appreciate an article like this. Most of the info here is gathered through my own experience, but I also used some text of various authors. I'll try to credit them at the end of my document. Please note that this is quite a huge document and errors are bound to enter here and there, both on the grammar level as the programming level. Forgive me for this, as I am not even close to Borg-perfection ;) As a last hint, I would strongly suggest to get a beer (more than one would be even better) when reading this article, coz it's kind of (very) dry. And I would even suggest going for whiskey straight when you get to the advanced part. (a bottle or three would suffice) <grin> I hope you will benefit from this, coz many seem to been requesting an optimizing tutorial to enter the Hugi vault of articles. 3. Introduction Many people claim that all programming nowadays should be done only at the highest possible level and let the compiler work out any given optimization to the code. Although this works in most applications, it is a considerable advantage to think about optimizing one's code at the design stage. Not only are there numerous applications out there that need the fastest possible code (especially in embedded environments), but also compilers are still made by people. And these people are responsible for the speed at which hundreds, if not thousands of applications will operate at when made with their compiler. This document is therefore written for those people who would like to know more about how to write speedy code or how to squeeze those extra few microseconds out of their algorithm. No matter what background they have, be it embedded application engineer, top-level software designer or a 13-year old demo-coder. ;-) 4. General optimization techniques 4.1 algorithm considerations A common misconception shared by many people is that the application you are developing will have the greatest speed when your code is fast and 50% written in assembly language. This is simply not true. First of all, an algorithm should be efficient and 'simple'. Simple does not mean your algorithm can not be complex. What is meant is that it should be readable and orderly maintainable. If your algorithm is poorly written, your implementation based upon it will be unreadable and by default slow in execution. (Definition of algorithm: A formula or set of steps for solving a particular problem. To be an algorithm, a set of rules must be unambiguous and have a clear stopping point. Algorithms can be expressed in any language, from natural languages like English or French to programming languages like C.) Secondly, it is unwise to think about a particular implementation language when designing your algorithm. Think about logical steps, which connect to your common life (to some extent). See yourself as the program, which should perform the various actions. (See figure 3.1 below.) For people who are too used to programming, it is suggested to make up some sort of pseudo-language for their own, which leans more towards algorithm design than to actual code (like C). 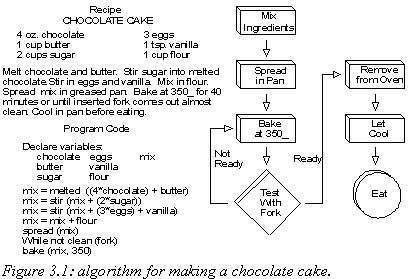As a last point, don't be afraid to TRY out things. Make some doodles on a piece of paper, especially for the more complex kind of algo's. Although most people find it time consuming and mostly useless, a diagram or flowchart can often proof a worthy companion when trying to design a nifty algorithm. There are many other things to do when designing an algorithm. And although this falls beyond the scope of this document, it is important to be aware of algorithm design methods. 4.2 Assembly versus high-level language, compiler considerations There are roughly said two big fronts in the software/embedded world. One who swears by what the compiler outputs as machine code, the other who holds strongly to his/her beliefs that the handwritten assembly code can beat any compiler in existence today. As with all things in life there is a golden mean in between the two worlds. Compilers have come a long way. We are now in the 21st century and it would be surprising if they wouldn't know how to efficiently optimize the programmer's code. The question remains to which extend will those optimizations take full advantage of the CPU it is compiled for? The only certain way to find out is to debug the code and see for yourself. Many compilers for well-known older CPU's (Intel x86, Motorola 68xxx and others) are gone through so many revisions and updates that they produce quite efficient code. However, compilers made for more recent CPU's still lack in real optimization simply because they are new and therefore not all features and exceptions are fully documented, both for CPU and for compiler. As time progresses, new 'tricks' are discovered and added to the compiler heap of various techniques to output fast code. And by the time the CPU is dead old, the compiler will be nearly perfect. So, how to solve this everlasting problem? One idea proposed by many, is to implement the entire program in assembly so it will give the best possible results. Besides the fact that this will yield best results, it is not always feasible to dedicate so many hours in writing and optimizing a whole algorithm in pure assembly code. It might also be a total waste of time to optimize a part which deals with slow I/O transfers where the bottleneck in execution is the waiting for the I/O to finish and not the algorithm itself. You can sense the direction where this is leading. Only optimize those parts of your algorithm in assembly where the advantage would be the greatest. Therefore it is almost always an advantage to handcraft the inner loops in assembly and leave the surrounding code as is... Use the high-level language as a director to guide everything in good paths and let the assembly do the real work. 4.3 What's hot and what's not I've taken the liberty to make a list over the years of general optimization techniques for both the C and Assembly language. To make clear what's the difference between good and evil optimization, I've put them into a table, wickedly called "what's hot and what's not". 4.3.1 In C/C++ What's hot What's not x=0; if( x!=0 ) x=0; #define result(a,b) (((a)-(b))*((b)+1)) int result(a,b) { a = a-b ; b++; a = a * b; return a; }; REASON: For a small calculation like this one (or for example an "absolute" function), it is better to make a define out of it (=macro) so it will be compiled within the code instead of making a 'call' for it (which has to push values on the stack and so forth, which is slower in execution). for(I=0;I<100;) { Dostuff(I++); Dostuff(I++); ... Dostuff(I++); } for(I=0;I<100;I++) { Dostuff(I);} REASON: Two reasons apply here: (1) the pipeline is filled - (2) 'hot' code only does a few CMP's (which are relatively slow), while the 'not' code has to do 100 of them. for(I=0;I<MAX;I++) { for(j ...)A[I][j]=5; B[I][j]=0; } for(I=0;I<MAX;I++) for(j ...) A[I][j]=5; for(I=0;I<MAX;I++) B[I][j]=0; REASON: only one main 'for'-loop, no re-initialisation of variables. I=MAX+1; while (--I) {...} for(I=1;I<=MAX;I++) {...} REASON: This is actually one for braindead compilers. Most compilers will optimize this loop the best they can... It basically forces the compiler to use "DJNZ (decrease and jump if not zero)" instead of "ADD, CMP, JNE (jump if not equal)". Or on x86, it can just initialize CX with the "MAX" value and the put a "LOOP" instruction at the end. (which is the general DJNZ instruction for x86 specific.). REMARK: This can only be used if you want 'something' to be done MAX times. If you actually going to use 'I' in a calculation which depends on the order (0,1,2, ..., MAX), like for(I=1;I<=MAX;I++) table[I]=(table[I-1]<<1); it is best to use the normal form. (Or think how you can rewrite the loop to use the 'while' form.) for(j ...) { printf(h); h += 14; } for(j ... ) { h = 14 * j; printf(h); } REASON: Most CPUs have a slow MULtiply instruction. Adding is always much faster than multiplying. *temp = a -> b -> c[4]; Total = temp -> d + temp -> e; Total = a -> b -> c[4] -> d + a -> b -> c[4] -> e; (Another one for braindead compilers.) REASON: temp will be a pointer (A0 for motorola freaks, ES for x86 freaks :)). The 'hot' code can then use a simple offset to get the value. The 'not'-code has to calculate the pointer (and the offset) twice. do B; if(condition) { undo B; do A; } if( condition ) { do A; } else { do B; } REASON: Only valid if 'condition' doesn't happen often, and both A and B are small things and not for example intense AI calculations. X = y * y; X = pow(y,2.0); REASON: The pow-function invokes the floating point unit. Slow for a simple integer multiply instruction like this one. If you know that y is always an (2exp(n)) number, you can do the following: X = 1 <<(n<<1); Z = (y<<5) + y; Z = y * 33; REASON: shift and add are quicker than one mul instruction. X = y & 31; X = y % 32; REMARK: You have to be careful with this one. This only applies if you want to take a "2exp(n)" mod of any number. So 2,4,8,16,32,64,128,256, etc are all ok. REASON: Calculating a 'modulus' of a number, invokes a division. Most CPUs store both quotient and remainder when calculating a division. Division is therefore slower than multiplication. So a simple AND is much faster than division. X = y << 3; X = y * 8; REASON: shifting is quicker than multiplying. Can only be done when you want to multiply with a 2 exp(n) number (with n belonging to the natural numbers). X = (y + z) / w X = y/w + z/w REASON: Here you only have to do one division instead of two. This looks simple, but you often stumble into doing it the 'not' way. if( ((a-b) | (c-d) | (e-f))==0 ) {...} if( a==b && c==d && e==f ) {...} This is a hard one: sometimes the left is better, sometimes the right. Check assembly listing of how the compiler interpreted this one. REASON: The 'not' code normally compiles as: CMP JNE CMP JNE CMP JNE (jump over the code if not equal). CMP instructions are rather slow and a JNE also takes longer for the branch prediction, because most of the time the branch is not taken (see advanced section to read about branch prediction). So doing 3 SUB, 2 OR and a JNZ (over the code) is quicker. However, the 'not'-code could also be compiled as (a AND (NOT b)) OR (c AND NOT(d)) OR (e AND NOT(f)) JNZ (over the code), which is quicker than the above. if( x & 5 ) {...} if( (x & 1) || (x & 4) ) {...} REASON: Simple binary "math" can explain this. And one instruction is better than 3. if( ((unsigned) (x|y) < 8 ) {...} if( x>=0 && x<8 && y>=0 && y<8) {...} REASON: binary math again: after the or, we can see at bit 3 if one of them exceeds the boundaries. if( x&(x-1)==0 && x!=0 ) {...} if( (x==1) || (x==2) || (x==4) || (x==8) || ...) {...} REASON: we know that the value to be checked has to be a 2exp(n), so binary math again. Even better is "if (!(x&(x-1)) && x)", which only has one JNZ. if( (1<<x) & ((1<<2) | (1<<3) | (1<<5) | (1<<7) | (1<<11) | (1<<13) | (1<<17) | (1<<19)) ) {...} if( (x==2) || (x==3) || (x==5) || (x==7) || (x==11) || (x==13) || (x==17) || (x==19) ) {...} REASON: the "((1<<2) | (1<<3) ...)" will be compiled as one constant. So one shift, an "AND" and a JZ is much quicker than many CMP x, <value> and the OR's. static long abs(long x){ long y; y= x >> 31; Return (x^y)-y; } #define abs(x) (((x)>0)?(x):-(x) REASON: Debate is possible on this type of optimization, but here you just do simple (pipelined) archimetic code and no jumps. Jumps flushes the pipeline and cause processor stalls in the execution units. typedef stuct { Int element[3][3][3]; } Three3Dtype; Three3Dtype a,b; b=a; memset(a,0,sizeof(a)); int a[3][3][3]; int b[3][3][3]; ... for(I=0;I<3;I++) for(j=0;j<3;j++) for(k=0;k<3;k++) b[I][j][k]=a[I][j][k]; for(I=0;I<3;I++) for(j=0;j<3;j++) for(k=0;k<3;k++) a[I][j][k]=0; REASON: if you don't see the use of this, you better stop coding altogether. ;-) for(tx=1,sx=0,x=0;x<100;x++) { if( tx<=x ) { Tx += (sx<<1) + 3; Sx++; } printf("%d\n",sx); } for(x=0;x<100;x++) { printf("%d\n",(int)(sqrt(x))); } EXPLANATION: The main idea this is: The sum of the N first odd integers is equal to the square of N. Formula: E(i=0,i=(n-1)) (2i+1) = n^2 (sum of (2i+1) with i ranging from 0 to (n-1) ) Example: N=8: The first 8 odd integers are: 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 = 64, which is the same as N^2 = 8^2 = 64. Proof by use of substitution: Let's suppose it is true for a number called (n-1). (plain substitution of (n-1) in the formula) E(i=0,i=(n-1)) (2i+1) = [E(i=0,i=(n-2)) (2i+1)] + [2(n-1)+1] = (n-1)^2 + 2n - 2 + 1 = n^2 - 2n + 1 + 2n - 2 + 1 = n^2 (so it is proven) So it is easy to deduce some sort of reversed algorithm that searches how many odd numbers (let's call this X) you must add before you reach the number N. X is by definition the integer square of N. The reason why I use "Tx += (sx<<1) + 3;" instead of "Tx += (sx<<1) + 1;" is that I take the "E(i=0,i=n)" instead of (n-1) so I automatically "skip" one iteration by doing "+3" instead of "+1". PS: Mind the () around "(sx<<1) + 3" ! ANSI C gives higher priority to addition than to shifting!! (Which is wrong IMO... shifting is in essence MUL or DIV.) unsigned int x,y,a; ... a = (x & y) + ((x^y)>>1); unsigned int x,y,a; ... a = ( x + y ) >> 1; /* overflow fixup */ if( a < x && a < y ) a+=0x80000000; REASON: The if is a branch instruction. It can cause a stall and is rather slow due to the CMP+branch. The left side is a simple integer operation and quick in execution. Use a power of 2 in multidimensional arrays. A[2^n][2^m] A[10][11] Lookups in pre-calculated tables Calculate everything with each iteration Copy pointer Copy entire tables Sort structs: longest type first and keep same types together Dump all kind of things in structs without thinking Use merge sort or radix sort Use quicksort algorithm Get examples from the Internet and look in various newsgroups Look through (school) notes for suggestions Get suggestions but be skeptical Ignore all suggestions from others Think, code, think, code ... Code, code, code, code ... 4.3.2 In Assembly It is simply impossible to define general methods in assembly language due to architectural implications and the large variety of different processors, from RISC to CISC to hybrids. Therefore I leave it up to the reader to implement various (if not all) the previous techniques from the C section into the assembly language for the desired CPU with maximum use of register instead of memory variables. There are three techniques that can be implemented in assembly on almost any processor: code/data alignment, cache optimization and speedup of integer instructions. The first two being tightly interconnected. · Code/data alignment. To speed up the instructions, alignment of code should be on the beginning of cache boundaries. Thus, start your routine on the start of the cache page. This way, when someone calls the routine, the processor will just have to load a cache line to get the first sequence to feed into the CPU's pipeline (more on pipelines in the advanced section), and while they are executing it will have enough time to load the other cache lines needed. This will speed up the processing of all the instructions within that page. Misaligned access in the data cache causes extra cycles when reading/writing from/to that data. Ways to speed up data: For DWORD data, alignment should be on a 4-byte boundary. For WORD data, alignment should be on a 2-byte boundary. For 8 byte data (64 bits), data should be aligned on a 8-byte boundary so it is possible to use BURST READS/WRITES. In general, it is best to align data on a 2^n byte boundary. And yes, on many applications with tight inner loops, these things do accumulate to make a noticeable speed-up. BURST READS/WRITES: A data transmission mode in which data is sent faster than normal. There are a number of techniques for implementing burst modes. In a data bus, for example, a burst mode is usually implemented by allowing a device to seize control of the bus and not permitting other devices to interrupt. In RAM, burst modes are implemented by automatically fetching the next memory contents before they are requested. This is essentially the same technique used by disk caches. The one characteristic that all burst modes have in common is that they are temporary and unsustainable. They allow faster data transfer rates than normal, but only for a limited period of time and only under special conditions. Example: a common method for burst read/write is to transfer data both on the rising and falling edge of a clock signal, instead of only the rising edge as in normal operations. · Cache optimizations The difference between a cache hit and a cache miss means lots of CPU cycles lost, so better hit the cached locations to the max. Use "short" loops so there is more probability that the code to execute will reside fully into the cache. Then remember you can often count on an external cache of at least 64k (usually 128k...1024k for more recent CPUs). So, if you have to process big arrays or big bitmaps with multiple passages do not "scan" all the array for every pass, use a "strip by strip" strategy instead so every "strip" fully fits into the cache and is ready for the second and third pass without cache misses. This technique is called STRIP-MINING; you can include into your program a routine that checks the optimal "strip size" trying a multi-pass test on 64k, 128k, 256k, 512k strips and "complete array" and then sets the optimal "strip size" to use when performing "strip-mining" routines. On a Pentium, for example, you can use 8k "strips" so your "strip mined" routines will work with the full speed of the internal data cache (remember the internal cache works at full CPU speed while the secondary cache may be running at half that, or even lower). The advantage of strip mining is caused by the fact that the additional jumping/looping needed to process arrays in "strips" of adjacent memory locations that can fit together into the cache is a lot less than the time caused by a single cache miss. · Speedup for integer instructions 1. Avoid using complex instructions. Simpler instructions will get the job done faster. Simpler instructions have been getting faster with every new processor that has come along. 2. With 8-bit operands, do your best to use the byte opcodes, rather than using the 32 bit instructions with sign and zero extended modes. Internal sign extension is expensive, and speed increases can be found by simplifying the process as much as possible. 3. LEA's (Load Effective Adress) generally increase the chance of AGI's (Address Generation Stalls, see the advanced section). However, LEA's can be advantageous because: - In many cases an LEA instruction may be used to replace constant multiply instructions (a sequence of LEA, add and shift for example). - LEA may be used as a three/four operand addition instruction. LEA ECX, [EAX+EBX*4+ARRAY_NAME] - Can be advantageous to avoid copying a register when both operands to an ADD are being used after the ADD, as LEA need not overwrite its operands. The general rule is that the "generic" LEA A,[B+C*INDEX+DISPLACEMENT] , where A can be a register or a memory location and B,C are registers and INDEX=1,2,4,8 and DISPLACEMENT = 0 ... 4*1024*1024*1024 or (if performing signed int operations) -2*1024*1024*1024 ... + (2*1024*1024*1024 -1 ) , replaces the "generic" worst-case sequence MOV X,C ; X is a "dummy" register MOV A,B MUL X,INDEX ;actually SHL X, (log2(INDEX)) ADD A,DISPLACEMENT ADD A,X So using LEA you can actually "pack" up to five instructions into one! Even counting a "worst case" of two or three AGIs caused by the LEA, this is very fast compared to "normal" code. What's more, CPU registers are precious, and using LEA you don't need a dummy "X" register to preserve the value of B and C. 4. Zero-Extension with short ints terror tales The MOVZX takes four cycles to execute due to due zero-extension wobblies. A better way to load a byte into a register is by: xor eax,eax mov al,memory As the xor just clears the top parts of EAX, the xor may be placed on the OUTSIDE of a loop that uses just byte values. The 586+ shows greater response to such actions. It is recommended that 16 bit data be accessed with the MOVSX and MOVZX if you cannot place the XOR on the outside of the loop. 5. When comparing a value in a register with a constant, use a logical command like AND. On some processors, this is faster than a COMPARE or TEST instruction. 6. Address Calculations Pull address calculations into load and store instructions. Memory reference instructions have 4 operands: a relocatable time segment base, a base register, a scaled index register and a displacement. Often several integer instructions can be eliminated by fully using the operands of memory addresses. (More on this later.) 7. Integer divide In most cases, an Integer Divide is preceded by a CDQ instruction. This is as divide instructions use EDX:EAX as the dividend and CDQ sets up EDX. It is better to copy EAX into EDX, then arithmetic-right-shift EDX 31 places to sign extend. The copy/shift instructions take the same number of clocks as CDQ, however, on 586's they allow two other instructions to execute at the same time. If you know the value is always positive, use XOR EDX,EDX. However, on the Pentium 2/3, the CDQ is one micro-ops, compared to the multiple micro-ops of the copy/shift instruction. See my little note(s) at the end of this document. So for P2/3 CDQ is preferable. 8. Integer multiply The integer multiply by an immediate can usually be replaced with a faster and simpler series of shifts, subs, adds and lea's. As a rule of thumb when 6 or fewer bits are set in the binary representation of the constant, it is better to look at other ways of multiplying and not use integer multiply. (The thumb value is 8 on a 586.) A simple way to do it is to shift and add for each bit set, or use LEA. Here the LEA instruction comes in as major CPU booster, for example: LEA ECX,[EDX*2] ; multiply EDX by 2 and store result into ECX LEA ECX,[EDX+EDX*2] ; multiply EDX by 3 and store result into ECX LEA ECX,[EDX*4] ; multiply EDX by 4 and store result into ECX LEA ECX,[EDX+EDX*4] ; multiply EDX by 5 and store result into ECX LEA ECX,[EDX*8] ; multiply EDX by 8 and store result into ECX LEA ECX,[EDX+EDX*8] ; multiply EDX by 9 and store result into ECX And you can combine LEA's too: lea ecx,[edx+edx*2] ; lea ecx,[ecx+ecx*8] ; ecx <-- edx*27 (Of course, if you can, put three instructions between the two LEA so even on Pentiums, no AGIs will be produced.) 9. Clearing Registers Using "XOR reg,reg" is fast but sets up conditions codes. A slightly slower way to do it of course is to mov reg,0, which preserves condition codes. 10. Jump instructions Jump instructions come in two forms, one real near that jumps between -127 and 128 of the current location, and a 32 bit version that does a full jump. The short form is quite a bit faster, however unfortunately many compilers put long jumps where short jumps would suffice. To ensure that short jumps can be used (when you know it is possible), explicitly specify the destination as being byte length (i.e. use jmp short instead of plain jmp, if you can). 11. Task Switching Task Switching is evil. It is slow, real slow. Avoid task switching too often, as more and more of your time will be spent in processing the task switch. For faster task switching, perform your task switching in software. This allows a smaller processor state to be saved and restored. Anything that shaves time of 75+ clock cycles isn't all that bad in my book. 12. Minimize segment register loads and the use of far pointers as dearly much as you can. If you are doing a lot of processing on a small piece of data far away, it might be faster just to copy the data to nearby and work on it there (by the way, this is a good reason to use flat protected mode on x86 CPUs). 5. Advanced Optimizations (ok... on to the whiskey :)) This section is for the more advanced readers, who know already about general optimizations and wish to learn more complex methods of increasing the speed of their inner loops. As those inner loops are mostly programmed in assembly language, it is difficult to explain various techniques without giving clear examples. Therefore all following examples will be given for the Intel Pentium processor, as this is a wellknown CPU used in many of toady's applications (be it in desktop, server or embedded systems). All generations following the Pentium (Pentium MMX, Pentium Pro, Pentium II, Celeron, Pentium III, Celeron2 and the Pentium IV) benefit from the same optimizations explained here, as well as AMD's K5, K6, K6-2, K6-3 and the newer Athlon family of processors. Many of the technology used in the Pentium, is also implemented on numerous other CPUs. For example: many consider the Motorola 68060 the equivalent of the Intel Pentium, because it has almost all of same features: - pipelines for integer and floating point units - superscalar pipeline and dual execution units - branch prediction units - memory management units - code and data caches You can feel that on each of these features, a dedicated optimization technique can be applied to speed up execution time considerably. The ideas and methods that will be explained in the examples here, can be easily ported to any other CPU that has one or more of these features. 5.1 Pipeline optimization It is extremely important for this advanced section that the reader is totally familiar with pipeline execution. It is because of this that a complete explanation of pipeline processing and its dangers is given before any methods for improving speed in pipeline CPUs is discussed. · What is pipelining? The execution of a machine code instruction can be roughly split in five stages: [n.b. this is a generic pipeline] 1) FETCH instruction opcode and immediate data 2) DECODE opcode and align immediate data into temporary registers 3) CALCULATE ADDRESS OF OPERANDS and load 'em into memory. (calculate the address of memory locations to access and select the register operands to use - sometimes called DECODE 2) 4) EXECUTE instruction (loading memory operands if needed) & write results to INTERNAL registers 5) WRITEBACK memory-operand results to memory Every stage takes one or more CPU cycles to be completed, but usually a modern CPU needs just one CPU cycle for every execution stage (excluding stages 1 and 5 that have to deal with memory/cache access and stage 4 when "complex" microcoded instructions are executed). A CPU-core (the "real" CPU, not cache support nor the other things that are usually integrated into a modern CPU) has five "specialized" units, one for every stage of instruction execution, plus a "register file" (and ultra-fast on-chip memory where internal register values are stored) and a control unit. The control unit "coordinates" the action of all the other units so they can work together. MEMORY INPUT ("memory load" unit) ¦ +------------+ +------->+------------+<-------->¦ ¦ +++ ¦ FETCH ¦ ¦ ¦ +---------------------+¦+>+---------------+ ¦ ¦ ¦ (instruction pointer)¦ ¦ ¦ ¦ ¦ ¦ +------------+<-+ ¦ ¦ ¦ ¦ ¦ DECODE ¦<-------->¦ ¦ ¦ ¦ +---------------+ ¦ ¦ ¦ ¦ ¦ ¦ ¦ ¦ ¦ +------------+<-+ ¦ CONTROL ¦ ¦ ++ ¦ ADDRESS C. ¦<-------->¦ ¦ ¦ +----+-->+---------------+ ¦ UNIT ¦ ¦ ¦ ++ ¦ ¦ ¦ +------------------------+ +->+------------+<-+ ¦ ¦ ¦ REGISTER FILE +----->¦ EXECUTE ¦<-------->¦ ¦ +------------------------+<---------------------+ ¦ ¦ ¦ ¦ ¦ +------------+<-+ ¦ ¦ ¦ WRITEBACK ¦<-------->¦ ¦ +---------------+ ¦ ¦ ¦ +------------+ MEMORY OUTPUT <---+ ("memory store" unit) If you look at the drawing, the control unit needs to communicate with all the other units to make them work together. Usually the "control unit" is scattered in little units that coordinates instruction and data flow between adjacent units, but you can think about it as a single independent unit. The five execution units are what gives the "raw" CPU power but the control unit is what lets you fully utilize them. Let's suppose every unit performs one operation in one step. With a "cheap" control unit, to execute a complete machine language instruction you first enable FETCH, then you enable DECODE and so on until WRITEBACK is completed and the control unit enables FETCH again to execute the next instruction. This is what happens into an "absolutely not pipelined" CPU with "one cycle" stages, the fastest instructions takes 5 cycles and the control unit is very simple (just a circular shift register that enables one unit at a time). Of course this is the worst case and nobody is so lame to build a CPU like that. Every CPU stage-execution unit is a stand-alone thing, it has its hardware and its "temporary registers" so it is capable to operate "alone". So, if the control unit can synchronize the operations of all the stage-execution units, it can make them work in pipeline. It is much as in a factory, where every worker/robot in a production line: a) receives a partially refined product from the previous worker in line b) performs some simple operations to refine the product a little more c) pass the result to the next worker in line A CPU with such a control unit is called a pipelined CPU. If you have to execute in sequence instructions A, B, C, D, E on a pipelined processor.... While the WRITEBACK unit is performing stage 5 of A the EXECUTION unit can perform stage 4 of B the ADDRESS CALCULATE unit can perform stage 3 of C the DECODE unit can perform stage 2 of D and the FETCH unit can perform stage 1 of E So if you start the CPU at instruction A it looks like that instruction A takes 5 cycles while instructions B, C, D, E (immediately one stage behind) looks like they take just one cycle! If you execute a sequence of 8 instructions on a "not pipelined" processor with a five stage "pipe" it takes 40 steps to execute the sequence, while on a pipelined processor this takes 5+7=12 steps! (5 steps for the first instruction to get through the pipeline then 7 steps for the other instructions immediately "one step" behind.) And the more instructions are executed in sequence, the more it looks like every instruction takes "just" one cycle to execute. This is of course the optimal situation, where the processor pipeline is filled and when every instruction does not use memory/register operands "still under processing" in successive execution-stages. · How to optimize your code to take advantage of the pipeline? Generally spoken, it is best to know what things a CPU 'checks' to make a pipeline work correctly. The pipelined processor control-unit must 'check': a) at stage 1 (FETCH) IF in stage 2..4 there are JUMP instructions [they change the program counter (the same register used by the fetch unit)] THEN stage 1 must wait (stall) until the jump is completed and then "restarts", loading the memory location pointed by the new program counter value. Because the jump opcode must pass through the decode stage ... ... if the DECODE unit "detects" a jump opcode, it makes the FETCH unit "stops" at least for two cycles until the jump is performed. This of course means the processor pipeline "wastes" some CPU cycles. b) at step 3 (ADDRESS CALCULATION) IF in stage 3 a register needed for address calculation is under processing in stage 4 (EXECUTE) THEN the stage 3 unit generates a "do nothing" control sequence for one CPU cycle. c) memory access conflicts These can be caused by lots of different things, they are usually resolved by the memory load/store units. Told in a short way, in a fully pipelined processor when the pipeline is "working on a sequence" the first instruction in the sequence takes the full execution time while the other instructions takes a shorter time (usually one cycle) because they are immediately behind, this means they "look faster" (and in fact they are, because the pipeline fully utilizes all the functional units it has). If some instructions "modify" values needed in the previous CPU stages the control unit stops the unit needing those values (and the others behind it) and inserts "do nothing" codes into the successive units in the processor pipe to make things work as expected (this is called a pipeline stall or a pipeline flush). This explains why usually a taken jump takes more time than one that's not taken (when a jump is performed you must flush the pipeline). The newer processors include JUMP PREDICTION UNITS that handles jump faster, but the less you jump, the better. So in order to optimize your code to fully take advantage of the pipeline, you should reorder your instructions in the inner loop carefully. Sometimes an unlogical order sequence of instructions might proof to be faster than a more human-readable approach. C-example: Consider a 4-stage fully pipelined processor that really needs the following code to be as fast as possible: int sum = 0; int f[100]; int j; for ( j = 0 ; j < 100 ; j++ ) sum += f[j]; After compilation, one can clearly see that in the assembly listing, a value is added to the 'Sum' and then a check is made if all the 100 values have been added. If not, an index register is incremented and a jump is made so another value is added. Clever readers might have guessed that this is absolutely not favorable for a 4-stage pipeline CPU. Because any kind of jump flushes the pipeline. If the "addition" instruction took 4 cycles to complete, the time to calculate the entire sum would take approx. 400 cycles. The right way to implement this routine : int sum1,sum2,sum3, sum4, sum, j; int f[100]; sum1=sum2=sum3=sum4=sum=0; for ( j = 0 ; j < 100 ; j += 4 ) { sum1 += f[j]; sum2 += f[j+1]; sum3 += f[j+2]; sum4 += f[j+3]; }; sum = sum1 + sum2 + sum3 + sum4; In this implementation, the pipeline is fully used and the time to calculate the sum is 4 (for the first add) + 99 (for the 99 following adds) + (4+3) (last sum) = 110 cycles. A performance gain of roughly 4 over the previous implementation! Addendum: For all you Intel freaks: The new Pentium 4 has a 20 (yes, twenty) stage pipeline, which could explain why performance is so low in today's applications (which are optimized for Pentium 2/3 which have a smaller pipeline). All applications are optimized for a P2/3 pipeline (based on the PentiumPro core), especially loops. So, for example, after a few instructions optimized for P2/3 pipeline (which fits nicely in their pipeline), a "jump not equal" is seen and the huge 20-stage pipeline is flushed and has to be filled all over again, for every iteration of the loop. A little note on the side: I think AMD is sure gonna win in pure performance in today's applications. I'm purely basing myself on benchmarks made by many many people and hardware sites. In almost every test, a lower clocked Athlon CPU beats the Intel CPU. Hehe, even a 1.2GHz Athlon can beat the Pentium4@1.7GHz with not much problem. But, as I said, that's for today. 'Tomorrow' may be a totally different story. Software optimized for 20-stage pipelines will really rock (pipelines are cool, just admit it :)) And the SSE2 is also pretty damn impressive (just go check out the specs on the Intel site). Nice... Today AMD, tomorrow Intel, isn't it just great to be living in these times? 5.2 Superscalar pipeline optimization. All superscalar processors have the feature of having two or more pipelines that can work concurrently. Our Pentium has two, which we call the U-pipe and the V-pipe. The 68060 has also 2, but are called "pOE" and "sOE". Please refer to the manual of your CPU to check how the pipelines are organized. Both the U en V pipe are a full 5-stage pipeline, but with small differences: only some instructions can be executed in the V-pipeline, and others only in the U-pipeline, and some can be executed in both. It is important that you are aware of these instructions. Look them up in a reference manual and keep them at hand when you are about to optimize your inner loops. The main advantage of a dual-pipeline architecture is that it can give a performance gain of factor 2 in most circumstances, because 2 instructions can be executed simultaneously per clock. (This is called pairing.) The idea to get the most out of your code, is to make sure that as much instructions as possible are executed in parallel. The criteria for dual pipeline execution is: 1. Both instructions must be simple (see below). 2. There must not be a read-after-write or write-after-read register/flag dependencies between them. 3. Neither can have a displacement and an immediate. 4. Instructions with prefixes can only occur in the U-pipe (except for branches on condition jz, jc, etc. etc.). The following are considered "simple" instructions, the ALU means any ALU command (ADD, SUB, AND, etc): 1. mov reg, reg/mem/immed 2. mov mem, reg/imm 3. ALU reg, reg/mem/immed 4. ALU mem, reg/immed 5. inc reg/mem 6. dec reg/mem 7. push reg/mem 8. pop reg 9. nop 10. lea reg/mem 11. Jmp/ Call / Jcc near Remember only the U pipe can perform SHIFTS/ROTATIONS so "couple" every shift/rol with a simple instruction before and after to be sure every pipeline is filled. Note, however, that while both pipelines can perform ALU instructions concurrently, this is not the case when one ALU instruction requires the output of the other pipeline ALU instruction. Example: ALU instruction in pipe U and performing ADC in pipe V. There are two exceptions to this rule: a) In the case of a compare/branch combination. b) With push/pop combinations (because of optimized stack access). Example of pairing advantages: C-code: void ChangeSign (int * A, int * B, int N) { int i; for (i=0; i<N; i++) B[i] = -A[i]; } Compiled ASM-code (x86): _ChangeSign PROCEDURE NEAR PUSH ESI PUSH EDI A EQU DWORD PTR [ESP+12] B EQU DWORD PTR [ESP+16] N EQU DWORD PTR [ESP+20] MOV ECX, [N] JECXZ L2 MOV ESI, [A] MOV EDI, [B] CLD L1: LODSD NEG EAX STOSD LOOP L1 L2: POP EDI POP ESI RET _ChangeSign ENDP This looks like a nice solution, but it is not optimal because it uses slow non-pairable instructions. It takes 11 clock cycles per iteration if all data are in the level one cache. _ChangeSign PROCEDURE NEAR MOV ECX, [N] MOV ESI, [A] TEST ECX, ECX JZ SHORT L2 MOV EDI, [B] L1: MOV EAX, [ESI] ; u XOR EBX, EBX ; v (pairs) ADD ESI, 4 ; u SUB EBX, EAX ; v (pairs) MOV [EDI], EBX ; u ADD EDI, 4 ; v (pairs) DEC ECX ; u JNZ L1 ; v (pairs) L2: POP EDI POP ESI RET _ChangeSign ENDP Here we have used pairable instructions only, and scheduled the instructions so that everything pairs. It now takes only 4 clock cycles per iteration. A speed increase of 250%! It is clear that superscalar pipeline optimization has a significant impact on execution speed. However, as technology progresses, it becomes more difficult to implement these optimization methods, because some CPUs nowadays have no less than 6 or more concurrent pipelines and handwriting your code for these CPUs can be a complicated task. 5.3 Branch prediction The Pentium attempts to predict whether a conditional jump is taken or not. It uses a 'branch target buffer' (BTB), which can remember the history of 256 jump instructions. The Pentium without MMX makes the prediction on the basis of the last two events. It guesses that a conditional jump will be taken if it was taken the previous time or the time before. It guesses that the jump is not taken if it was not taken the last two times. A conditional jump which has not been seen before (or is not in the BTB) is predicted as not taken. The Pentium with MMX (and the PentiumPro) makes its prediction on the basis of the last four events, so that it is able to predict a simple repetitive pattern. A conditional jump which has not been seen before (or is not in the BTB) is predicted as taken if it goes backwards (e.g. a loop), and as not taken if it goes forward. If a conditional jump is properly predicted (i.e. if the guess was correct) then it takes only one clock cycle. A mispredicted branch takes 4 clock cycles if it is in the U-pipe and 5 clock cycles if it is in the V-pipe. The penalty for misprediction is doubled or tripled if another jump or call follows in the first clock cycle after the mispredicted branch. The first two instructions after a possibly mispredicted branch should thereforee not be branch, jump, or call instructions. You may put in NOP's or other instructions to avoid this. The Pentium with MMX may also have a penalty in this case, but only if the two consecutive branch instructions end within the same aligned dword of memory. This problem may be avoided by using a near displacement rather than short on the second branch instruction to make it longer, but this method doesn't help on the Pentium without MMX so you should rather put in some NOP's or other instructions. The jump prediction algorithm is optimal for a loop where the testing is at the bottom, as in this example: MOV ECX, [N] L: MOV [EDI],EAX ADD EDI,4 DEC ECX JNZ L Since the jump prediction algorithm for the Pentium without MMX is asymmetric, there may be situations where you can improve performance by reordering your code. Consider for example this if-then-else construction: TEST EAX,EAX JNZ SHORT A1 CALL F0 JMP SHORT E A1: CALL F1 E: If F0 is called more often than F1, and F1 is seldom called twice in succession, then you can improve jump prediction on the Pentium without MMX by swapping the two branches. However, this will be slightly suboptimal on the Pentium with MMX and the PentiumPro because they may mispredict the branch if it is not in the branch target buffer. Another tradeoff is that the code cache is used less efficiently when the seldom used branch comes first. You may put in two NOP's before each of the CALL instructions here to avoid the penalty of a call after a mispredicted jump. Indirect jumps and calls through function pointers will be poorly predicted on the Pentium with MMX and the PentiumPro. Avoiding branches to optimize execution time Sometimes it is possible to obtain the same effect as a branch by ingenious manipulation of bits and flags. For example you may calculate the absolute value of a signed number without branching: (as mentioned in the what's hot and what's not table). MOV EDX,EAX SAR EDX,31 XOR EAX,EDX SUB EAX,EDX The carry flag is particularly useful for this kind of tricks. Setting carry if a value is zero: CMP [value],1 Setting carry if a value is not zero: XOR EAX,EAX / CMP EAX,[value] Incrementing a counter if carry: ADC EAX,0 Setting a bit for each time the carry is set: RCL EAX,1 Generating a bit mask if carry is set: SBB EAX,EAX This example finds the minimum of two unsigned numbers: C-code: if (b < a) a = b; ASM-code without branches: SUB EBX,EAX SBB ECX,ECX AND ECX,EBX ADD EAX,ECX This example chooses between two numbers: if (a != 0) a = b; else a = c; CMP EAX,1 SBB EAX,EAX AND ECX,EAX XOR EAX,-1 AND EAX,EBX OR EAX,ECX Whether or not such tricks are worth the extra code depend on how predictable a conditional jump would be. On some CPUs, you can use conditional move instructions to obtain the same effect. 5.4 Pitfalls Here follows a short list of common pitfalls when programming in assembly language. It concentrates on the various possibilities to stall the CPU and lose a couple of valuable cycles, which could have been used for instruction execution. Note again that these common stalls are known to exist on every CPU, which has pipeline processing. (The examples use x86 assembly instructions.) · Address generation stalls (AGI) An 'Address Generation Interlock' occurs when a register, which is currently being used as the base or an index, was the destination component of a previous instruction. For example: add edx, 4 // AGI, ONE CLOCK STALL mov esi, [edx] For the 486, AGI's can only occur on adjacent instructions and on the 586 or Pentium instructions up to 3 locations away can cause an AGI. (I.e. an instruction waiting to execute step 4 on pipeline 1 may need to wait the result produced by an instruction still executing on pipeline 2.) pipeline step pipe1 pipe2 address_calculate/fetch_operand C D execute B A If C needs the results of A, it must stall pipeline 1 for one cycle to wait for A to "exit from" pipeline 2. If C needs the results of D, it must stall pipeline 1 for two cycles to wait for D to "exit from" pipeline 2. An example of 3 instruction away AGI: add esi, 4 pop ebx dec ebx mov edx, [esi] Takes 4 clocks on a 486. On a 586, the move command must wait for the add command, thus AGI stalling for one clock. The code above then would run in three clock cycles on a 586. Remember that even instructions that read or write implicitly to registers cause AGI stalls: mov esp,ebp pop ebp is executed as... mov esp,ebp [agi] ; pop uses the esp as a pointer pop ebp · Instruction decoding stalls When decoding an instruction with an immediate value and either an index offset or an immediate displacement, some CPUs have a one clock penalty. Example: mov spam, 248 mov dword ptr [esp+4], 1 This happens because the decode stage of the pipeline can read and decode one "immediate" value at a time while an immediate value and an immediate offset are TWO immediate values. · Register access CPU stalls (only on some CPUs) 486's have a 1 clock penalty when modifying the lower word of a DWORD register that's used immediately after it, 586's do not. Example: mov al,0 mov [ebp], eax (a one clock penalty on 486, no penalty on a 586) 6. SIMD-emulation This part is about a technique developed when implementing a cryptographic function, which was quite slow, even on a 32 bit processor. The code was based on the fastest known algorithm in the field, but still didn't yield favorable results. Even after applying all known optimization techniques as described in this document, execution time was still very high. I was more and more wishing to have a fast SIMD CPU instead of the relative slow 32bit processor with which I had to work with. SIMD stands for "Single Instruction, Multiple Data" and it means that a single instruction can read/modify/write multiple, independent, data in a single clock cycle. Popular SIMD instructions are known as MMX, 3DNow!, SSE and SSE2. 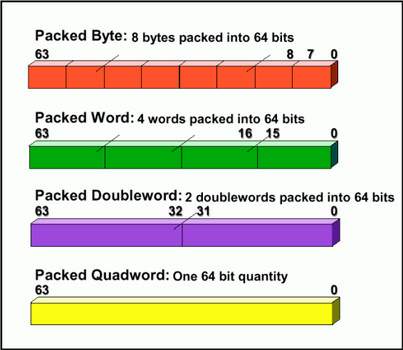An example of a MMX data representation (MMX registers are 64 bits wide): With only one special MMX instructions I can load an array of 8 bytes into a 64bits register and then multiply each byte by a certain number (let's say 23) with just one instruction: (mm0 is one of the 64bit registers.) (pseudo code!!) Movq mm0,[array] Pmulb mm0, 23 Movq [array],mm0 This gives an increase of at least factor 8 for the execution time compared to the implementation of loading each of the 8 bytes in a register, multiply this register by 23 and then writing the result back to the [array+index]. And no one is stopping you from implementing the same trick on a non-SIMD CPU. To prove this, I will explain how I managed to improve execution time for a function from 6 milliseconds to 0.6 milliseconds. A factor of no less than 10! This trick is not only valid for cryptographic routines, but can be applied to every routine that does a lot of calculations and it is not a complex technique at all. With cryptographic functions, a lot of calculations are done on individual bytes. 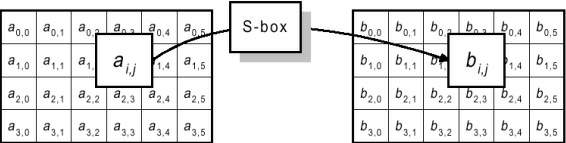In reference documents, they are normally viewed upon as matrices on which some kind of algorithm is applied to which results in a new matrix: Here, the so-called "S-box" is a certain function which transforms one byte into another. Let us say that for this example the S-box function is: b(i,j) = a(i,j) * 2; if (overflow) b(i,j) = b(i,j) (xor) 0x1B; When applying optimization, one cannot go further than replacing the 'multiply by 2' by a 'shift left by 1 position', because there has to be checked for an overflow and depending on that, the result can be different. Furthermore, the table had a strange structure. Look at the procedure below which implemented the S-box algorithm. 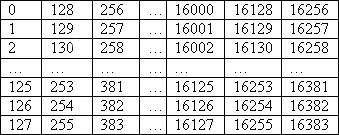unsigned char Table_A[128][128]; unsigned char Table_B[128][128]; unsigned char x,y; unsigned int temp; /* temp is 32 bits wide */ for(x=0;x<128;x++) for(y=0;y<128;y++) { temp=(unsigned int) Table_A[y][x]; temp*=2; If(temp > 255) { temp &= 0x000000FF; /* AND is faster than SUBB 255d */ temp ^= 0x0000001B; } Table_B[y][x] = (unsigned char) temp; } So the 2 dimensional array was as follows: In memory, this is ordered like this: 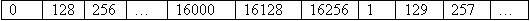Which is not only difficult to implement an optimization, but also extremely bad for CPU's with a small cache line (for example 32 bytes) because for every new byte fetched, there is a cache miss. (RAM is definitely not random access when cache is used!) We only do a calculation on every 128th byte in memory. Consider the following piece of code: unsigned char Table_A[128][128]; unsigned char Temp_Table[128][128]; unsigned char Table_B[128][128]; unsigned char x,y; unsigned int temp; /* temp is 32 bits wide */ for(x=0;x<128;x++) for(y=0;y<128;y++) Temp_Table[x][y] = Table_A[y][x]; for(y=0;y<128;x++) for(x=0;x<128;y++) { temp=(unsigned int) Temp_Table[y][x]; temp*=2; if(temp > 255) { temp &= 0x000000FF; /* AND is faster than SUBB 255d */ temp ^= 0x0000001B; } Table_B[x][y] = (unsigned char) temp; /* reverse x and y so result is */ /* written in the right place for B */ } Although this code seems slower because it is more lengthy, it is not because there are no cache misses anymore and therefore no CPU stalls to fetch a new cache line out of main memory. 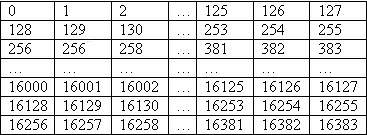So the 2 dimensional array is now as follows: In memory, this is ordered like this: Now that all the bytes are in a consecutive order, we can try to find a trick that can calculate multiple bytes with as few instructions possible. We must know what kind of CPU we are working on. In this case, a Motorola 68040 CPU was used. This is a 6-stage pipeline, 32bit, Big Endian processor. With a 32bit processor, we can cleverly modify 4 independent bytes at a time. Let's look at the algorithm again: b = a << 1 if(overflow) b = b ^ 1Bh - Multiplying 4 bytes with 2 is easy. Load a 32bit register with 4 consecutive bytes. Reset the most significant bit of each byte and shift the whole register left by 1 position. Example in C: unsigned char array[128]; unsigned long temp; *(unsigned long*) (array) & = 0x7F7F7F7F; temp = *(unsigned long*) (array) << 1; (most compilers will generate code that makes use of a register) - Doing a check for possible overflow is a bit harder, but a little hint can be found above. If the MSB of the byte is set, then we must multiply this byte with 1Bhex after the shift. Example in C: unsigned char array[128]; unsigned long temp2; /* detect bytes that need to be xor'd */ temp2 = ((*(unsigned long*) (array) & 0x80808080) >> 7) * 1B; If byte 1, 2 and 4 will give an overflow, temp2 will be 0x1B1B001B. - As a last step, we can simply XOR the two values (temp and temp2) to obtain a 4 byte result. - Written as one C statement, where x is the 32bit register which contains the 4 bytes: x = ((x & 0x7f7f7f7f) << 1) ^ (((x & 0x80808080) >> 7) * 0x1b); You might want to optimize the "multiply by 0x1B" if your compiler does not do this. 1Bhex = 27dec x * 27 = [((x<<3)-x)<<2]-x which are 4 simple instructions which can be executed very fast on most 32bit CPUs. With this information, we can construct the following pipeline optimized, SIMD-emulated routine for the S-box: unsigned char Table_A[128][128]; unsigned char Table_B[128][128]; unsigned char Temp_Table_A[128][128]; unsigned char Temp_Table_B[128][128]; unsigned char x,y; unsigned int temp; /* temp is 32 bits wide */ typedef unsigned long DWORD /* DWORD is 32 bits type */ /* First reorder table, so the bytes are consecutive in memory */ for(x=0;x<128;x++) For(y=0;y<128;y++) Temp_Table_A[x][y] = Table_A[y][x]; for(x=0;x<16384;x+=4){ /* load 4 bytes */ temp = *(DWORD*) (Temp_Table_A + x); /* Do calculation on 4 bytes in parallel */ temp = ((temp & 0x7f7f7f7f) << 1) ^ (((temp & 0x80808080) >> 7) * 0x1b); /* store 4 bytes in temperary output array */ *(DWORD*) (Temp_Table_B + x) = temp; } /* reorder output to comply with reference documents */ for(x=0;x<128;x++) for(y=0;y<128;y++) Table_B[x][y] = Temp_Table_B[y][x]; One last step was to rewrite the inner loop purely in assembly. That way I made sure that registers were used as much as possible and only the bare essential memory fetches were made. I also made sure the pipeline was not stalled and filled at all times. The results were impressive... 6. Conclusion It is obvious that there are many optimization techniques that can improve execution time considerably. I hope that the methods explained in this document are clear and that they will help you to improve old and new code to run as efficient as possible. Feel free to send me feedback. Happy coding. Extra Notes: Before I switch off my computer to go biking, I wanted to give some extra information about several things: - Everything here is applicable when you are working with any kind of 32bit CPU. - Almost everything can be applied when working with Pentiums & compatibles. - Most (general) things can be applied with success when dealing with PentiumPro, Pentium2, Pentium3, K6-x and Athlon architecture, but these CPUs are internally quite different than any previous CPU. They actually work with micro-ops (µops) which are decoded instructions (out of a MUL for example). Some optimizations here are not discussed with the existence of those µops in mind. Don't worry though… Whatever CPU you have, your code won't go slower if you apply any kind of optimization described in this document. :) If enough people think this was a good document and found that I did a reasonable good job at explaining these topics, I'll write a document on optimizing specifically for the new breed of CPUs (from pentium2/K6 upwards). (With full explanation of µops e.o.t.) Credits: Nutfreak/Freedom Systems (this document) Gaffer/PRoMETHEUS (for the small collection of P5 optimizing docs) Agner Fog (pairing integer instruction hints) Michael Kunstelj & Lorenzo Micheletto (cache & pipeline hints) The Internet :) (http://www.azillionmonkeys.com/qed/optimize.html) (Inspiration for the what's hot, what's not) The Commodore 64 :) :) Nutfreak/Freedom systems