But let's be more pragmatic. How exactly could you profit from learning about Linear Algebra? First, you will understand why all these 3D things work. Don't say that you need only the final formula to get the effect working. Yes, probably after a couple of days filled with hacking and debugging it will work. But when you understand all the facts you are dealing with, the things are simpler to code and debug, really. So, the first aim: UNDERSTANDING! If I was a teacher I'd require my students not to learn all things by heart, but just to understand most of them.
When you understand something you can deduce some formulae again, if you have forgot them. Also, when you understand something, you can create another great thing on the base of this thing. So, another benefit: ability to create the NEW THINGS!
And the third benefit is the ability to simplify some things, proofs etc. In this article I will show two examples.
These are three main ways of profiting from Linear algebra, and oh!, why only L. A.? From any subject. So, I think that if you dare to call yourself a graphics coder, you simply must know L. A.
So, now examples come. The things you can deduce easily with Linear Algebra.
1) And, again, why does the rotation matrix look exactly this way and not another?
First of all, I'm not a 3D coder at all. So, don't expect something great from me, I'm here only to give you the base of such things and some basic examples, you should do everything other for yourself.
I simply wanted to deduce this matrix; while preparing for the exam on L. A. I even didn't remember it by heart. So, I simply lay on bed with a pen and a sheet of paper and found it, almost automatically. For less than 5 minutes, using the methods of L. A. Then I searched in Hugi and found a similar article by Dendrite in Hugi 15. And... I was surprised at the length of the proof! It covers several screen pages full of formulae! I'm ready to swear that this took Dendrite about half an hour to deduce, if not more. This is the place where school math leads you. To huge proofs. And that is why you should learn L. A. My proof isn't bigger than ten simple formulae. Let's look at it:
Start.
This picture will guide us:
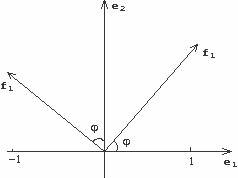
For beginners:
{basis = vectors of coordinate system}
Let's say we have a natural basis, e1 = (1;0); e2 = (0;1).
f1, f2 - our new, wanted basis; the angle between e1 and f1 is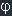 
.
e1 and e2 are normalized (their lengths are equal to 1).
(length = sqr(scalar multiplication) = sqr((e1, e1)) = sqr(1*1 + 0*0) = 1)
f1, f2 will also be normalized (because the rotation operator is an orthogonal operator and an orthogonal operator keeps orthonormed vecors orthonormed).
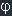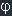f1 has the following coordinates: (cos; sin) (from the unite circle).
Using trigonometric formulae:
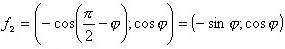
so, f1 = (cos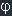; sin)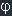
f2 = (-sin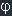; cos)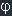
Let's write a matrix of transformation basis e to f. We know that it consists of the coordinates of basis f in coordinates of basis e written as columns. Now we know them. Let's write the matrix.
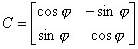
And that's all - absolutely strict and mathematical.
We know that if we take x expressed as a linear combination in basis f and multiply C on it, we will get x in the old basis, in e, so X(rotated, in e) = C * X(normal, in f).
Finished.
So, if to drop all explanations, which aren't necessary, it will contain no more than 10 lines. Really simple!
2) Pythagoras' theorem.
Theorem:
If a and b are orthogonal vectors (the angle between them is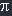 
) then |a+b|^2 = |a|^2 + |b|^2.
Comment: |x| means the length of vector x. As most of the time it is equal to sqr(scalar multiplication of vector on itself), scalar multiplication in an orthonormed basis can be defined as:
(x, y) = x1 * y1 + x2 * y2 + ... + xn * yn
where x1 ... xn are the coordinates of x and y1 ... yn are the coordinates of y.
So, |a| = sqr(a, a) = sqr(a1 * a1 + a2 * a2) = sqr(a1^2 + a2^2).
Comment 2: This theorem is nothing more nothing less than a simple school theorem, which is transformed to be true for vectors. In the formulation a and b are vectors, of course, not numbers!
Proof:
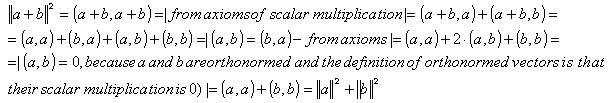
End of proof.
How do you like this tiny proof?! When I remembered what we had learned at school when we had deduced this theorem... I understood why I hadn't understood nothing back then.
But this proof is really easy to understand only if you know the axioms and definitions.
So, the main point,
"Er.. guy, what have you just written for us??? We can't get nothing!"
If this is the point, then you NEED to learn Linear Algebra! You see, everything is simpler and shorter with it, you only have to know some basic definitions to understand all of this.
Linear Algebra is simple, I guarantee! Anyway, it is much simpler than Math Analysis, for example.
So, what book should you read to learn algebra? In case you are lazy, and don't want to go to the library: I've written a special article, or it would be more correct to say a series of articles. The first chapter from this series you will find in this issue! Read it, I've worked hard, with the wish to give a good level of material, where everything is explained well.
Good luck!
ANY questions: iliks@chat.ru