Auditory localisation and its exploitation by surround sound systems

Dendrite/Hugi

To predators and prey alike, detection and localisation of sounds is vitally important for survival. Evolutionary pressures have led to humans and most animals being very good at localising the direction of a sound source in space. While the majority of the human population no longer uses this inherent skill to ensure survival by hunting, auditory localisation still pervades many aspects of everyday life, such as turning towards a person who starts speaking to oneself in a crowd, where e.g. visual input would be of limited use.

In the world of multimedia computing, 3D environments projected onto a 2D screen can be made more immersive at a reasonable cost by providing one sensory fraction of the third dimension through surround sound. With 3D graphics cards having paved the way, hardware rearmament has now reached the world of sound. Plummeting prices, growing popularity and support by software developers will ensure that surround sound is not just a temporary phenomenon.

The direction of a sound source can be defined by two angles measured from the mid-point between both ears:

- an angle of azimuth in the horizontal plane (straight ahead=0º, exactly to the right=90º and so on), and

- an angle of elevation (again, zero is in front, 90º immediately above etc.) in the mid-sagittal plane.

Under optimal conditions (sound source of broad frequency composition roughly in front of the subject), localisation is accurate to 1-2 degrees of azimuth and about 10 degrees of elevation.

The greater degree of precision in the the horizontal plane reflects the fact that humans keep their ears level at most times, and that their environment often approximates to a plane. This fact is certainly not unknown to developers of surround sound systems, and thus most common systems operate by a number of speakers in the horizontal plane only. Strictly speaking, they do not provide 3D, but 2D sound. However, little perceptual information is lost by omitting the vertical dimension in which localisation is of poor accuracy anyway. Furthermore, one could argue that visual and auditory information complement each other since the plane of the screen and the plane in which the speakers are arranged are perpendicular.

High accuracy localisation

High accuracy localisation involves binaural mechanisms: the central nervous system (CNS) compares the sounds received by the two ears and detects differences in intensity and time of arrival.

a) Interaural time differences (ITD)

For all directions other than the mid-plane (0º azimuth) sound has to travel further to reach one ear and so arrives later. The path difference (DL), and hence the time difference, varies with the angle of azimuth (q).

For humans, the maximum time difference, determined by head size, is about 660ms (at 90º or 270º azimuth) and the minimum detectable interaural delay, determined by limitations of the CNS, is about 10ms.

For periodic sounds, the extra path length also causes a phase shift. Phase comparisons become ambiguous above 1.5kHz: as the wavelength is decreased below the magnitude of the head, the phase difference exceeds one cycle, yielding several possible values for the phase shift.

Determining the corner frequency

c	speed of sound	300ms^(-1)
f	corner frequency	to be determined
l	wavelength/diameter of head	0.2m

c	   =	   f*l
300ms^(-1) =	   f*0.2m
f	   =	   1500Hz

Assuming that the head is spherical, the difference in path length is easily determined.

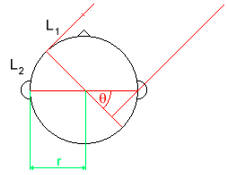
path difference = DL = L1 + L2

L1 = r sin q
L2 = r q		 (given that q is measured in radians)

DL = r (q + sin q)

The actual ITD can then be calculated:

ITD = DL / c

As noted above, phase differences are no longer useful when the frequency exceeds 1.5kHz. Fortunately, a different mechanism fills this gap. As the frequency rises above 1.5kHz, the wavelength becomes shorter than the magnitude of the head. The head is effective at screening such frequencies: the more distant of the two ears is shadowed from the sound source and consequently detects a lower intensity.

The interaural intensity difference is both a function of azimuth and of frequency. While the effects are small at low frequencies, an IID of 20dB is reached at 6kHz. This is more than enough, since it has been shown experimentally that the minimum detectable IID is around 1dB.

Note that the frequency at which shadowing starts depends on the size of the head. It may be due to this physical limitation that smaller animals (e.g. rodents, bats) have higher upper frequency limits than humans.

Cones of confusion

So far only variations in the angle of azimuth have been considered. But the angle of elevation also generates interaural time and intensity cues. The same set of time and intensity cues is possessed by a source at many positions. If the observer consists only of a spherical, bodiless head with symmetrical pinnae, a sound source may lie on any point on a conical surface whose apex is at the ear.

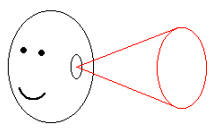
This conical surface is called a cone of confusion.

However, everyday experience tells us that accurate localisation is possible. Cones of confusion do in fact not exist because of the asymmetry of the head, the complex shape of the pinnae, and the shadowing effect of the body. These filter the sound reaching the ear depending on the direction of the source. Early in life one learns to associate a given sound coloration with a particular direction. This mechanism also accounts for the limited monaural localisation ability we possess.

A major limitation of auditory localisation in humans becomes evident when sounds are presented in the mid-plane. A sound source immediately in front may be located immediately behind and vice versa. This is due to the symmetry of the body about the mid-plane. Some animals have evolved particularly asymmetric ears to counteract this. Others can even move their ears, not only abolishing unwanted effects due to symmetry but also allowing for a higher general accuracy of localisation.

Distance determination

This is another weak area. Increasing the distance between the sound source and the observer has two effects:

- the amplitude of the sound decreases according to an inverse square law, and

- the spectrum is progressively filtered of high frequencies as these are more easily screened by small obstacles.

These effects are relative, so that they do not benefit the observer unless he is aware of the original sound amplitude and spectrum, as may be the case for e.g. speech.

Other factors

No normal environment behaves like a sound-absorbent chamber. There are always reflections of sound waves as determined by the surrounding objects and their acoustic properties. While they does not affect auditory localisation in any way other than perhaps degrading its accuracy, reflections do greatly contribute to the perception of the space one is in.

Reflections occupy the whole range from crisp echoes to diffuse reverberations. While their properties are beyond the scope of this article, it is worth noting that the industry is now shifting from merely providing a choice of ambient characteristics (e.g. Creative Labs' EAX 1) to more accurate modelling of obstacles between the source and the observer (Aureal's A3D 2.0). Eventually, acoustic raytracing will offer virtually perfect realism.

Lastly one should consider the actual sounds one is using. Their spectrum should contain the frequency range of the localisation mechanism(s) one is exploiting. Also the quality of the sounds should be good in order to justify the effort put into their postprocessing. A little play with that compressor and EQ might work magic.

The message is clear: surround sound can greatly add to a 3D atmosphere, but one should not overlook the importance of lower level influences.

Dendrite/Hugi