Heap Sort
Dario Phong/Hugi
Introduction
In this article we'll talk about heap sort, a sorting algorithm which
is O(N*(Log2(N))). All the ideas behind
heap sorting will be fully explained, so you only need programming experience
to understand this article.
Binary trees
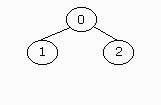
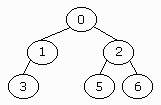
 A binary tree is a recursively defined data structure, it contains the
first node (called root node) and left and right sub-trees, which both are
binary trees, so they can also have left and right sub-trees. Usually a
node contains a symbol and two pointers, one to the left sub-tree and the
other one to the right sub-tree. If a pointer of a node is 0 then it has
no sub-tree. If a node has neither a left nor a right sub-tree, then it's a leaf
(like 3).
A binary tree is a recursively defined data structure, it contains the
first node (called root node) and left and right sub-trees, which both are
binary trees, so they can also have left and right sub-trees. Usually a
node contains a symbol and two pointers, one to the left sub-tree and the
other one to the right sub-tree. If a pointer of a node is 0 then it has
no sub-tree. If a node has neither a left nor a right sub-tree, then it's a leaf
(like 3).
The height of a binary tree is how deep the deepest leaf is. In the pic
on the right you can see a binary tree of height 2.
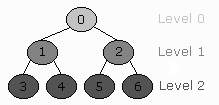
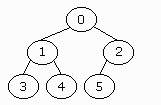
 A binary tree is completely full if its height is h and if it has 2h+1-1 nodes.
The binary tree on the right is a completely full binary tree. It has a
height of 2, so: (2*(2+1))-1=7, and this is the number of nodes which it
has. Note that the height of a completely full binary tree is log2(N),
where N is the number of nodes.
A binary tree is completely full if its height is h and if it has 2h+1-1 nodes.
The binary tree on the right is a completely full binary tree. It has a
height of 2, so: (2*(2+1))-1=7, and this is the number of nodes which it
has. Note that the height of a completely full binary tree is log2(N),
where N is the number of nodes.
A binary tree of height h is complete if it has one of the following properties:
1. It is empty.
2. Its left sub-tree is complete with height (h-1) and its right sub-tree
is completely full with height (h-2).
3. Its left sub-tree is completely full with height (h-1) and its right sub-tree
is complete with height (h-1).
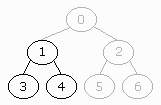
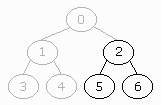
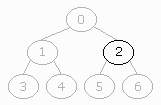
A binary tree is filled from left to right if all the leaves at the deepest
level are as far to the left as possible.
Once you understand all this theory about binary trees, you can understand
a heap.
Heap
A binary tree has the heap property if it has one of the following
properties:
1. It's empty. (Empty binary trees aren't very useful but they have all the
properties. E-))
2. The key of the root is higher than the ones from the sub-trees and the
sub-trees also have the heap property.
The key is the value which we use for sorting. Let me show some examples:
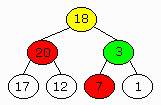
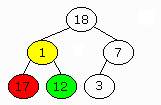
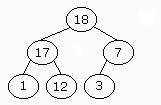
 The binary tree on the left is not a heap. Two nodes violate the heap
property. The key of the yellow node is 18, but its left sub-tree's key
is 20. The same goes for the green node with a key of value 3 and a sub-tree
with a higher value: 7.
The binary tree on the left is not a heap. Two nodes violate the heap
property. The key of the yellow node is 18, but its left sub-tree's key
is 20. The same goes for the green node with a key of value 3 and a sub-tree
with a higher value: 7.
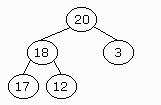
We can perform two operations with a heap: insertion and deletion. If
we want a binary tree to be a heap we must ensure the heap property every
time a symbol is added or deleted.
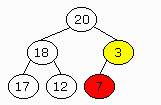
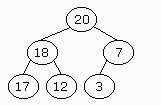
Insertion:
When we insert a new element we have to put it in the last position
(top to bottom and left to right) and move it up until the binary tree has
the heap property. In case it's inserted in the root we
have to perform no comparisons at all.
Deletion:
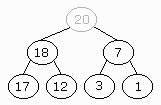
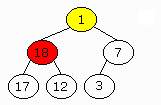
Once we have extracted the symbol with the highest priority (which is located
in the root) we have to delete it. We put the last element in its position
and exchange it with its child nodes until the binary tree is a heap. To
do so we have to follow some steps:
- Choose the higher child node (sub-tree).
- If its key is above the one from the current node we exchange them
and so on till the "new" symbol (we got it from the last position) has
child nodes which are lower than it.
As you can see the maximum number of swaps is h, which in fact is
log2(N), so both addition and deletion take
O(log2(N)). A heap may be used as a priority
queue.
Heap storage
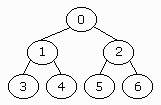
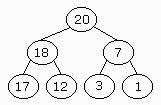
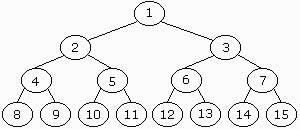 A heap is a complete binary tree filled from left to right, let's have
a look at it. Notice something? In fact the parent of a node with a key
k has the value k/2, the left child of this node has the key 2*k and
the right node has (2*k)+1. Look, the parent of the node with a k of 6
has a k of k/2=3, its left sub-tree is 2*k=12, and the right (2*k)+1=13.
A heap is a complete binary tree filled from left to right, let's have
a look at it. Notice something? In fact the parent of a node with a key
k has the value k/2, the left child of this node has the key 2*k and
the right node has (2*k)+1. Look, the parent of the node with a k of 6
has a k of k/2=3, its left sub-tree is 2*k=12, and the right (2*k)+1=13.
We can use this property for an efficient storage of a heap. The node
with value k will be in the position k in an array, so we don't need pointers,
just to keep track of the current position, usually we start at 1, and
then continue checking, so we only need to save in memory the symbols themselves.
Heap sort
If you've understood everything till there you have done 90% of heap
sort. Heap sort does the following:
- One pass over the data. Insert every element.
- Second pass. Extract all the elements.
Nothing else, nothing more. The first pass is a loop of N itinerations
(where N is the number of symbols to sort) and every insertion may take
up to Log2(N), the extraction has the same
complexity, so the total complexity is O(2*N*Log2(N)),
which in big-Oh is O(N*Log2(N)).
Closing words
If you find any mistake in this article or want to improve something,
email
me.
Thanks to John Morris
for his good articles and help with sorting algorithms and complexity.
Contacting the author
You can reach me via email.
Also don't forget to visit my home page
where you can find more and better info. See you in the next article!
Dario Phong, Barcelona 24-Jul-1999
 A binary tree is a recursively defined data structure, it contains the
first node (called root node) and left and right sub-trees, which both are
binary trees, so they can also have left and right sub-trees. Usually a
node contains a symbol and two pointers, one to the left sub-tree and the
other one to the right sub-tree. If a pointer of a node is 0 then it has
no sub-tree. If a node has neither a left nor a right sub-tree, then it's a leaf
(like 3).
A binary tree is a recursively defined data structure, it contains the
first node (called root node) and left and right sub-trees, which both are
binary trees, so they can also have left and right sub-trees. Usually a
node contains a symbol and two pointers, one to the left sub-tree and the
other one to the right sub-tree. If a pointer of a node is 0 then it has
no sub-tree. If a node has neither a left nor a right sub-tree, then it's a leaf
(like 3).
 A binary tree is completely full if its height is h and if it has 2h+1-1 nodes.
The binary tree on the right is a completely full binary tree. It has a
height of 2, so: (2*(2+1))-1=7, and this is the number of nodes which it
has. Note that the height of a completely full binary tree is log2(N),
where N is the number of nodes.
A binary tree is completely full if its height is h and if it has 2h+1-1 nodes.
The binary tree on the right is a completely full binary tree. It has a
height of 2, so: (2*(2+1))-1=7, and this is the number of nodes which it
has. Note that the height of a completely full binary tree is log2(N),
where N is the number of nodes.
















 A heap is a complete binary tree filled from left to right, let's have
a look at it. Notice something? In fact the parent of a node with a key
k has the value k/2, the left child of this node has the key 2*k and
the right node has (2*k)+1. Look, the parent of the node with a k of 6
has a k of k/2=3, its left sub-tree is 2*k=12, and the right (2*k)+1=13.
A heap is a complete binary tree filled from left to right, let's have
a look at it. Notice something? In fact the parent of a node with a key
k has the value k/2, the left child of this node has the key 2*k and
the right node has (2*k)+1. Look, the parent of the node with a k of 6
has a k of k/2=3, its left sub-tree is 2*k=12, and the right (2*k)+1=13.